11 KiB
fplot module
This provides a rudimentary means of displaying two dimensional Cartesian (xy)
and polar graphs on framebuf based displays. It is an optional extension to
the MicroPython nano-gui
library: this should be installed, configured and tested before use.
This was ported from the
lcd160cr-gui library.
Like nanogui.py it uses synchronous code.
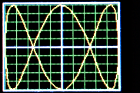
Please excuse the photography: these displays look much better than in my pictures.
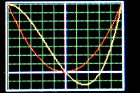
 Still from a simulation of plotting realtime data
using the
Still from a simulation of plotting realtime data
using the TSequence class.
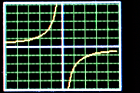
 Still from a simulation of realtime acquisition of
two varying vectors.
Still from a simulation of realtime acquisition of
two varying vectors.
Contents
- Python files
- Concepts
2.1 Graph classes
2.2 Curve clsses
2.3 Coordinates - Graph classes
3.1 Class CartesianGraph
3.2 Class PolarGraph - Curve classes
4.1 class Curve
4.1.1 Scaling Optional scaling of data values.
4.2 class PolarCurve
4.2.1 Scaling Required scaling of complex points.
4.3 class TSequence Plot Y values on time axis.
Main README
1. Python files
These are located in the plot directory.
fplot.pyThe plot libraryfpt.pyTest program. Usage examples.
Before attempting to use this library please install and test the nanogui
module on your hardware.
2. Concepts
Data for Cartesian graphs constitutes a sequence of x, y pairs, for polar
graphs it is a sequence of complex z values. The module supports three
common cases:
- The dataset to be plotted is complete at the outset.
- Arbitrary data arrives gradually and needs to be plotted as it arrives.
- One or more
yvalues arrive gradually. TheXaxis represents time. This is a simplifying case of 2.
2.1 Graph classes
A user program first instantiates a graph object (PolarGraph or
CartesianGraph). This creates an empty graph image upon which one or more
curves may be plotted.
2.2 Curve classes
The user program then instantiates one or more curves (Curve or
PolarCurve) as appropriate to the graph. Curves may be assigned colors to
distinguish them.
A curve is plotted by means of a user defined populate generator. This
assigns points to the curve in the order in which they are to be plotted. The
curve will be displayed on the graph as a sequence of straight line segments
between successive points.
Where it is required to plot realtime data as it arrives, this is achieved
via calls to the curve's point method.
2.3 Coordinates
Graph objects are sized and positioned in terms of TFT screen pixel
coordinates, with (0, 0) being the top left corner of the display, with x
increasing to the right and y increasing downwards. By nanogui convention
a border, if specified, extends two pixels beyond the graph in each direction.
If the graph is placed at [row, col] the top left hand corner of the border is
at [row-2, col-2]. The coordinate system within a graph conforms to normal
mathematical conventions.
Scaling is provided on Cartesian curves enabling user defined ranges for x and y values. Points lying outside of the defined range will produce lines which are clipped at the graph boundary.
Points on polar curves are defined as Python complex types and should lie
within the unit circle. Points which are out of range may be plotted beyond the
unit circle but will be clipped to the rectangular graph boundary.
Contents
3. Graph classes
3.1 Class CartesianGraph
Constructor.
Mandatory positional arguments:
writerACWriterinstance.rowPosition of the graph in screen coordinates.col
Keyword only arguments (all optional):
height=90Dimension of the bounding box.width=110Dimension of the bounding box.fgcolor=NoneColor of the axis lines. Defaults to Writer forgeround color.bgcolor=NoneBackground color of graph. Defaults to Writer background.bdcolor=NoneBorder color. IfFalseno border is displayed. IfNonea border is shown in theWriterforgeround color. If a color is passed, it is used.gridcolor=NoneColor of grid. Default: Writer forgeround color.xdivs=10Number of divisions (grid lines) on x axis.ydivs=10Number of divisions on y axis.xorigin=5Location of origin in terms of grid divisions.yorigin=5Asxorigin. The default of 5, 5 with 10 grid lines on each axis puts the origin at the centre of the graph. Settings of 0, 0 would be used to plot positive values only.
Methods:
clearNo args. Clears all curves from the graph.showNo args. Redraws the graph. For future/subclass use.
3.2 Class PolarGraph
Constructor.
Mandatory positional arguments:
writerACWriterinstance.rowPosition of the graph in screen coordinates.col
Keyword only arguments (all optional):
height=90Dimension of the square bounding box.fgcolor=NoneColor of the axis lines. Defaults to Writer forgeround color.bgcolor=NoneBackground color of graph. Defaults to Writer background.bdcolor=NoneBorder color. IfFalseno border is displayed. IfNonea border is shown in theWriterforgeround color. If a color is passed, it is used.gridcolor=NoneColor of grid. Default: Writer forgeround color.adivs=3Number of angle divisions per quadrant.rdivs=4Number radius divisions.
Methods:
clearNo args. Clears all curves from the graph.showNo args. Redraws the graph. For future/subclass use.
Contents
4. Curve classes
4.1 class Curve
The Cartesian curve constructor takes the following positional arguments:
Mandatory arguments:
graphTheCartesianGraphinstance.colorIfNoneis passed, thegraphforeground color is used.
Optional arguments:
3. populate=None A generator to populate the curve. See below.
4. origin=(0,0) 2-tuple containing x and y values for the origin. Provides
for an optional shift of the data's origin.
5. excursion=(1,1) 2-tuple containing scaling values for x and y.
Methods:
pointArguments x, y. DefaultsNone. Adds a point to the curve. If a prior point exists a line will be drawn between it and the current point. If a point is out of range or if either arg isNoneno line will be drawn. Passing no args enables discontinuous curves to be plotted. This method is normally used for real time plotting.
The populate generator may take zero or more positional arguments. It should
repeatedly yield x, y values before returning. Where a curve is discontinuous
None, None may be yielded: this causes the line to stop. It is resumed when
the next valid x, y pair is yielded.
If populate is not provided the curve may be plotted by successive calls to
the point method. This may be of use where data points are acquired in real
time, and realtime plotting is required. See function rt_rect in fpt.py.
4.1.1 Scaling
By default, with symmetrical axes, x and y values are assumed to lie between -1 and +1.
To plot x values from 1000 to 4000 we would set the origin x value to 1000
and the excursion x value to 3000. The excursion values scale the plotted
values to fit the corresponding axis.
4.2 class PolarCurve
The constructor takes the following positional arguments:
Mandatory arguments:
graphThePolarGraphinstance.color
Optional arguments:
3. populate=None A generator to populate the curve. See below.
Methods:
pointArgumentz=None. Normally acomplex. Adds a point to the curve. If a prior point exists a line will be drawn between it and the current point. If the arg isNoneno line will be drawn. Passing no args enables discontinuous curves to be plotted. Lines are clipped at the square region bounded by (-1, -1) to (+1, +1).
The populate generator may take zero or more positional arguments. It should
yield a complex z value for each point before returning. Where a curve is
discontinuous a value of None may be yielded: this causes plotting to stop.
It is resumed when the next valid z point is yielded.
If populate is not provided the curve may be plotted by successive calls to
the point method. This may be of use where data points are acquired in real
time, and realtime plotting is required.
4.2.1 Scaling
Complex points should lie within the unit circle to be drawn within the grid.
Contents
4.3 class TSequence
A common task is the acquisition and plotting of real time data against time, such as hourly temperature and air pressure readings. This class facilitates this. Time is on the x-axis with the most recent data on the right. Older points are plotted to the left until they reach the left hand edge when they are discarded. This is akin to old fashioned pen plotters where the pen was at the rightmost edge (corresponding to time now) with old values scrolling to the left with the time axis in the conventional direction.
The user instantiates a graph with the X origin at the right hand side and then
instantiates one or more TSequence objects. As each set of data arrives it is
appended to its TSequence using the add method. See the example below.
The constructor takes the following args:
Mandatory arguments:
graphTheCartesianGraphinstance.colorsizeInteger. The number of time samples to be plotted. See below.
Optional arguments:
4. yorigin=0 These args provide scaling of Y axis values as per the Curve
class.
5 yexc=1
Method:
addArgvthe value to be plotted. This should lie between -1 and +1 unless scaling is applied.
Note that there is little point in setting the size argument to a value
greater than the number of X-axis pixels on the graph. It will work but RAM
and execution time will be wasted: the constructor instantiates an array of
floats of this size.
Each time a data set arrives the graph should be cleared, a data value should
be added to each TSequence instance, and the display instance should be
refreshed. The following example assumes that ssd is the display device and
wri is a Writer or CWriter instance.
def foo():
refresh(ssd, True) # Clear any prior image
g = CartesianGraph(wri, 2, 2, xorigin = 10, fgcolor=WHITE, gridcolor=LIGHTGREEN)
tsy = TSequence(g, YELLOW, 50)
tsr = TSequence(g, RED, 50)
for t in range(100):
g.clear()
tsy.add(0.9*math.sin(t/10))
tsr.add(0.4*math.cos(t/10))
refresh(ssd)
utime.sleep_ms(100)